6. Tunelovanie elektrónov

V tomto príklade si vysvetlíme a spočítame kvantové tunelovanie elektrónov, aj keď po prečítaní tejto vety sa vám pravdepodobne dvíha žalúdok, tak vedzte že pravdepodoben zvládnete príklad spočítať a vždy môžete odovzdávať iba čiastočné riešenia. Pomôže nám to lepšie pochopiť zákony mikrosveta a princípy, na ktorom funguje scanning tunnelling microscope, stroj na skúmanie tenkých vrstiev materiálov.

Úvod

Najskôr si vysvetlíme, ako vyzerá interakcia vlny s povrchom materiálu. Vieme, že výchylku vlny, napríklad elektromagnetickej alebo aj vlny na hladine vody, možno popísať rovnicou: \[ \psi(x,t) = A\cos(kx - \omega t + \phi)\text{,} \]

kde \(A\) je amplitúda (napr. výška alebo intenzita elektrického poľa), \(\phi\) je fázový posun, \(\omega\) uhlová frekvencia, \(k = 2\pi/\lambda\) tzv. vlnové číslo, ktoré rastie so zmenšujúcou sa vlnovou dĺžkou \(\lambda\). Vzťah medzi \(k\) a \(\omega\) sa líši od systému, je iný pre vlny na vode, elektromagnetické žiarenie, ako aj pre elementárne žiarenie. Dokonca je iný aj pre rôzne častice v rôznych materiáloch. Efektívne v sebe skrýva informáciu o mechanizme interakcie daného objektu s danou látkou. Napríklad pre svetlo platí \(\omega = ck\), kde \(c\) je rýchlosť svetla a pre voľné elektróny \(\omega = \hbar k^2/(2m)\), kde \(\hbar\) je Planckova konštanta a \(m\) je hmotnosť elektrónu.

Elektrón ako vlnu popíšeme komplexnou exponenciálou, ktorá je všeobecnejšia ako kosínus. Amplitúdu položíme rovnú jednej a fázu nule, a predpokladáme, že vlna sa šíri smerom doprava: \[ \psi(x) = e^{ikx}\text{.} \]

Hybnosť elektrónu je \(p = \hbar k\), z čoho vychádza už spomínaná kinetická energia \(E= p^2/(2m) = \hbar k^2/(2m)\). Pre elektrón idúci doľava jednoducho otočíme znamienko: \(\psi(x) = e^{-ikx}\). Tiež sme vyhodili čas, pretože uvažujeme časovo nepremenný proces, t. j. elektróny pumupujeme nejakým strojom smerom doprava. Produkujeme teda nielen jeden elektrón, ale súvislý a konštantný tok.

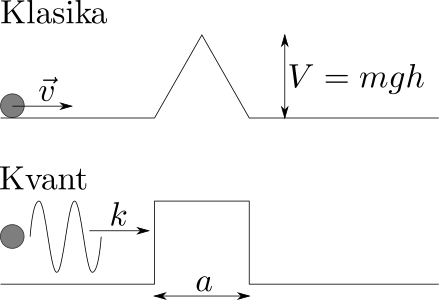
Keď takáto vlna narazí na prekážku, ktorej výška (meraná v energii, napr. v gravitačnom poli ako \(V = mgh\), viď.  ??) je nižšia ako kinetická energia elektrónu, časť vlny sa odrazí a časť prejde. Podobne, ako keď morská vlna narazí na útes, ktorý je nižší ako výška vlny. No v mikrosvete môže vlna prejsť cez prekážku aj v prípade, keď je energetická bariéra vyššia, odtiaľ výraz tunelovanie¹. Experimenty tento neintuitívny jav podporujú a tu si ukážeme, ako ho možno popísať.

Druhá mocnina vlnovej funkcie je rovná hustote pravdepodobnosti výskytu častice v priestore. Pre rovinnú vlnu platí \({|\psi(x)|}^2 = \psi(x)\psi^{*}\!(x) = 1\), a teda nachádza sa všade rovnako, keďže elektróny pumpujeme konštantným tempom).

Náš systém

Majme rovinnú vlnu \(\psi(x) = e^{ikx}\), ktorá zľava dopadá na bariéru o šírke \(a\) a energetickej výške \(V_0\). Základná vlastnosť vlnovej funkcie je energia, z ktorej môžno odvodiť vlnové číslo ako \(k = \frac{\sqrt{2mE}}{h}\).

Naším cieľom je zistiť ako bude vyzerať vlna, ktorá prejde do bariéry, ako aj tá, ktorá vyjde z bariéry. Máme teda tri tvary vlny:

1. naľavo, člen ktorý pumpujeme a odrazený člen s polomerom \(r\): \[ \psi_1(x) = e^{ik_1x} + re^{-ik_1x}\,\text{,} \]
2. v bariére: \[ \psi_2(x) = Ae^{ik_2x} + Be^{-ik_2x}\,\text{,} \]
3. a napravo, člen, ktorý sa šíri len doprava. \[ \psi_3(x) = te^{ik_1x}\,\text{.} \]

Máme tiež dva predpoklady:

1. Vlna je na rozhraní spojitá: \[ \psi_1(x = 0) = \psi_2(x = 0) \quad \text{a} \quad \psi_2(x = a) = \psi_3(x = a)\,\text{.} \]
2. Nemôže nastať skok v sklone vlny, teda aj prvá derivácia je všade spojitá. V opačnom prípade by vlna mala nekonečnú kinetickú energiu. \[ \psi_1'(x = 0) = \psi_2'(x = 0) \quad \text{a} \quad \psi_2'(x = a) = \psi_3'(x = a)\,\text{.} \]

Zadanie

1. Aké je vlnové číslo \(k_2\) pre vlnu vnútri bariéry? Je vždy reálne?
2. Vyriešte štyri rovnice spojitosti vlnovej funkcie a jej derivácie na rozhraniach o štyroch neznámych \(r, t, A, B\). Čomu sa rovná \(r\) a \(t\)?
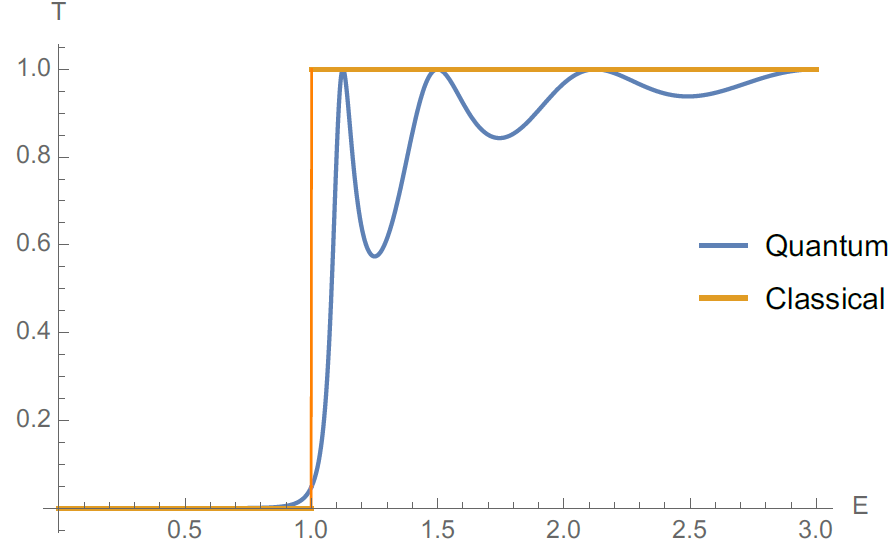
3. Veličina \(T = |t| = tt^{*}\) (transmisivita) udáva množstvo elektrónov, ktoré prejdú na druhú stranu bariéry za jednotku času, teda niečo ako prietok. Ako závisí \(T\) od energie elektrónov \(E\) na začiatku? Nakreslite túto závislosť od \(E/V_0 = 0\) po \(E/V_0 = 3\). Zvoľte fixnú šírku bariéry \(a = 2\pi.\)
4. Pre \(E > V_0\), ako možno vysvetliť lokálne minimá?