2. Blesk

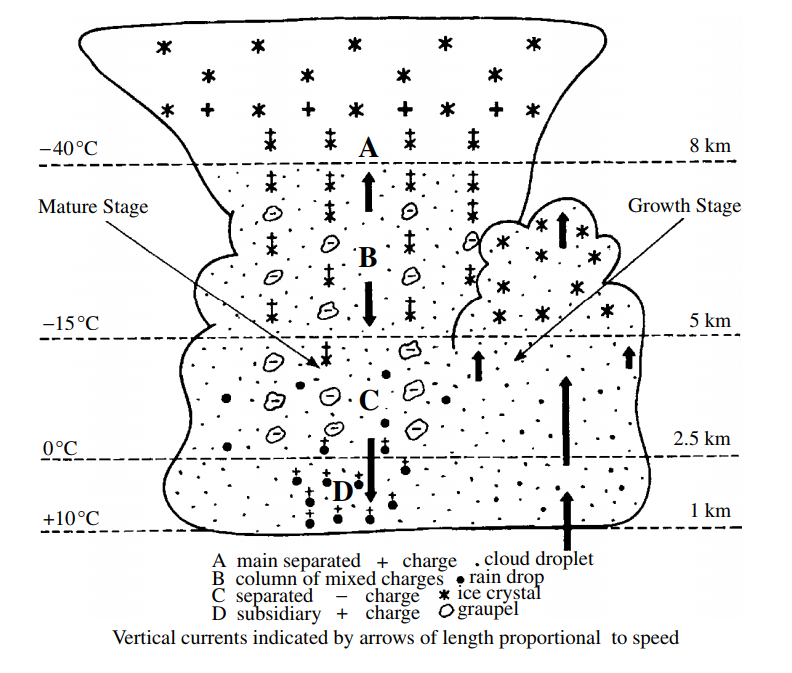
V tom príklade sa pokúsime odhadnúť ako súvisí množstvo zrážok, ktoré spadne na povrch Zeme s rýchlosťou ako sa nabíja oblak voči Zemi, a teda ako dlho potrvá kým udrie blesk. Teda to bude vašou úlohou :) Na priloženom obrázku môžete zhruba vidieť aké častice sa nachádzajú na rôznych miestach búrkového mračna. K hromadeniu náboja dochádza preto, lebo sa padajúce kvapôčky vody trú o častice ľadu a malé ľadovce (tzv. hail pelets a grapels), ktoré si môžeme pre jednoduchosť predstaviť ako dokonalé gule. V dôsledku tohoto procesu dochádza mechanickým spôsobom k indukovaniu elektrického náboja, vďaka čomu sa v oblaku po čase vytvorí kritické elektrické pole, v ktorom začnú ióny vo vzduchu viesť elektrický prúd.

Ľadovú guľu vo vonkajšom elektrickom poli \(E\) si môžeme predstaviť ako dokonale vodivú guľu, ktorá sa dodatočne polarizuje pod vplyvom elektrického poľa tak, že jej horná polovica je kladne nabitá a dolná polovica nabitá záporne. Ak sa ľadová čiastočka nabila na elektrický náboj \(-Q_R\), tak celkový náboj \(q_r\), ktorý sa prenesie pri styku ľadovca a kvapiek vody na kvapku vody s polomerom \(r\) je \[ q_r = \left(\frac{\pi}{2}E\varepsilon_0\cos\theta+\frac{\pi^2}{6}\frac{Q_R}{R^2}\right)r^2 \].

Rýchlosť nabíjania ľadovcov v oblaku (\(\mathrm{d}Q_R/dt\)) je úmerná koncentrácii kvapiek vody \(n_r\), prenesenému náboju pri jednej zrážke \(q_r\), rýchlosti padajúceho ľadovca \(V_R\) efektívnej relatívnej ploche \(\sigma = 0.74\), ktorú vidia kvapky narážajúce do ľadovca pod uhlom \(\theta\) meraného od „pólu“ ľadovca \(\alpha \pi R^2 =\frac{2r}{R}\frac{\sin\theta}{1-\cos\theta} \pi R^2 \approx 0.017\), pre realistické hodnoty polomeru kvapiek a ľadovca.

• Ukážte, že pre rýchlosť nabíjania platí z predchádzajúcej úvahy nasledujúca rovnica a vyriešte túto rovnicu pre \(Q_R(t)\).

\[ \frac{\mathrm{d}Q_r}{\mathrm{d}t} = -\sigma \alpha \pi R^2 V_R n_r q_r \]

V zvyšnej časti riešenia môžete predpokladať, že časová konštanta, ktorá sa objavila v riešení tejto rovnice je rovná \(\tau = {\left(\frac{\pi^3}{6}\sigma V_R n_r\alpha r^2\right)}^{-1} \approx \SI{150}{\second}\). Význam tejto konštanty udáva časovú škálu, na ktorej dochádza k nabíjaniu ľadovcov v mračne.

Nárast elektrického poľa v mračne je potom úmerný koncentrácii ľadovcov, ich rýchlosti pádu \(V_R\), a náboja \(Q_R\) sčítaného cez ľadovce všetkých môžných polomerov \(R\), \[ \frac{\mathrm{d}E}{\mathrm{d}t} = - 4\pi \int_R\mathrm{d}R N_R Q_R V_R\text{.} \] Naproti tomu je množstvo zrážok \(p\), ktoré dopadne za jednotku času úmerné \[ \frac{\mathrm{d}E}{\mathrm{d}t} = \int_R\mathrm{d}R \frac{4}{3}\pi R^3 N_R \rho_i V_R\text{.} \]

• Jednoduchou argumentáciou ukážte, že tieto vzťahy sú dobre motivované. Využitím všetkých rovníc a predpokladu, realistického nárastu množstva zrážok na začiatku búrky k maximálnej hodnote \(\SI{30}{\milli\metre\per\hour}\) za čas \(10\) minút, \[ p(t) = 30\left(1-e^{-t/600}\,\text{mm}\text{h}^{-1}\right)\text{,} \] nájdite čas, za ktorý udrie blesk po začatí búrky t.j. elektrické pole v oblaku dosiahne medznú hodnotu \(E = \SI{4270}{\volt\per\centi\metre}\) (tzv. prierazné napätie), pri ktorej sa stáva vzduch elektricky vodivým v dôsledku ionizácie. „Pokojové“ elektrické pole Zeme má hodnotu približne \(E_0 = \SI{5}{\volt\per\centi\metre}\).