2. Gravitačné vlny

V tejto úlohe sa pozrieme na objav gravitačných vĺn zo začiatku tohoto roka a pokúsime sa jednoduchým modelom založeným v princípe na rozmerovej analýze objasniť výsledky experimentu publikovaného v B.P. Abbott et al., Observation of Gravitational Waves from a Binary Black Hole Merger, Physical Review Letters 116, 061102 (2016).

Predpokladajme, že počas procesu spájania dvoch čiernych dier hmotností \(M\) a \(m\) sa čierne diery pohybujú v každom momente po kruhovej dráhe s polomerom \(R\) a \(r\) okolo spoločného hmotného stredu uhlovou rýchlosťou \(\omega\).

1. Nájdite \(\omega\) ako funkciu \(M\), \(m\), \(r\), \(R\) a \(G\), kde \(G\) je gravitačná konštanta.
2. Nájdite vzťah pre celkovú energiu systému ako funkciu \(\omega\).

Emisia gravitačných vĺn

Newtonova teória gravitácie nepredpokladá vznik gravitačných vĺn, ktoré by so sebou odnášali energiu zo systému. Na to, aby sme analyzovali proces spájania dvoch čiernych dier, musíme nájsť vzťah pre výkon prislúchajúci emisii gravitačných vĺn v systéme. Gravitačné žiarenie je emitované, keď sa príslušne pohybujú veľmi ťažké objekty, podobne ako elektromagnetické žiarenie emitované pri zrýchľovaní nabitých častíc. Pri vhodných podmienkach je pole gravitačného žiarenia dané zmenou kvadrupólového momentu rozdelenia hmotnosti, ktoré, ako sa ukazuje v našom prípade, sa redukuje na obyčajný moment zotrvačnosti \(I\), ktorý poznáme z mechaniky. Výkon radiačného žiarenia je úmerný kvadrupólovému momentu, konkrétne \[P \sim I^2\text{.}\]

Podobný vzťah nachádzame aj pri elektromagnetických vlnách, kde je hustota energie úmerná štvorcu intenzity elektrického resp. indukcie magnetického poľa. Očakávame, že výkon bude taktiež závisieť na frekvencii obehu čiernych dier \(\omega\) a fundamentálnych konštantách \(G\) a \(c\), kde \(c\) je rýchlosť svetla.

3. Rozmerovou analýzou nájdite príslušné hodnoty exponentov v nasledujúcom vzťahu \[ P = \alpha I^2\omega^{\epsilon}G^{\eta}c^{\rho}\text{.} \]

Bezrozmerná konštanta \(\alpha\) sa nedá nájsť rozmerovou analýzou. Všeobecná teória relativity dáva predpoveď \(\alpha = 32/5\). Dá sa ukázať, že uhlová frekvencia emisie gravitačných vĺn súvisí s obehovou uhlovou rýchlosťou ako \(\omega_{\text{vlny}} = 2\omega\).

4. Využitím predchádzajúceho výsledku a výsledku z časti \(b\) nájdite výraz pre \(\mathrm{d}\omega/\mathrm{d}t\).

Chirp

Pod slovíčkom chirp (https://en.wikipedia.org/wiki/Chirp) sa skrýva jav, pri ktorom postupne rastie frekvencia pozorovaného signálu v čase.

5. Na základe predcházajúceho výsledku nájdite vzťah medzi počiatočnou frekvenciou \(f_i\) a konečnou frekvenciou \(f_k\), ktoré pozorujeme v signáli interferometra pozorujúceho spojenie dvoch čiernych dier s príslušnými hmotnosťami \(m\) a \(M\) počas doby \(t\).

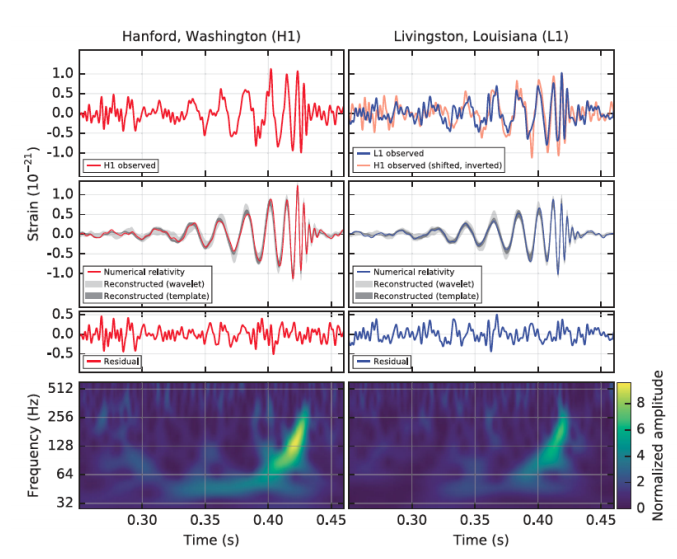
6. Výraz \((Mm)^{3/5}/(m+M)^{1/5} = \mathcal{M}\) nazveme hmotnosť chirpu \(\mathcal{M}\). Odhadnite hodnotu \(\mathcal{M}\) pri evente, vďaka ktorému sa podarilo overiť existenciu gravitačných vĺn, na základe grafu publikovaného v B.P. Abbott et al., Observation of Gravitational Waves from a Binary Black Hole Merger, Physical Review Letters 116, 061102 (2016), ktorý nájdete aj vyššie.

Spojenie čiernych dier

Schwarzschildov polomer je taká vzdialenosť od objektu, pri ktorej je úniková rýchlosť rovná rýchlosti svetla. Predpokladajme, že čierne diery sa spoja v momente, keď sa stretnú ich horizonty udalostí (polomer horizontu udalostí je pre čierne diery rovný príslušnému Schwarzschildovmu polomeru).

7. Využitím predchádzajúcich výsledkov a dát, ktoré môžeme vyčítať z priloženého grafu, odhadnite hmotnosti čiernych dier \(m\) a \(M\).
8. Využitím predchádzajúcich výsledkov a dát, odhadnite aj celkovú energiu \(E\), ktorá bola vyžiarená počas spájania čiernych dier vo forme gravitačných vĺn.
9. Výsledky, ktoré ste dostali vo všetkých úlohach, porovnajte so skutočnými výsledkami určenými experimentom LIGO.